UCAT Advice Decision Making
3 Common Decision Making Mistakes and How to Avoid Them
In this article, we’re going to discuss some common decision making mistakes and show you how to avoid them.
What are the common decision making mistakes that students struggle with?
Students that sit the Decision-Making subtest typically tend to struggle with the following:
- Personal bias: In the “Interpreting information” and “strongest argument” sections, there will be questions with incorrect answer options which will penalise subjective responses. These responses are often based on personal opinions instead of objective reasoning.
- Running out of time: The Decision-Making section requires students to complete a question every minute. This can be especially difficult when dealing with complex Venn diagrams or analysing large texts of information.
- Making assumptions: Student’s often struggle with exclusively using the information provided in the question/statement to arrive at logical conclusions. For example, when dealing with syllogisms or inference questions, a common mistake is to select responses that seem reasonable but involve one or more assumptions that are not justified by the stimulus.

How will this article help me?
In this article, we’ll:
- Provide detailed solutions to decision making questions that will outline what it looks like to come to logical conclusions based off the information given in the question.
- Explain what assumptions were behind the incorrect responses to help identify the causes of invalid conclusions.
- Identify sources of subjective bias in incorrect responses from the strongest argument subsection.
What is Decision Making and what are Venn Diagram and Strongest Argument Problems
The Decision Making Subtest is a challenging section that requires you to answer 29 questions in 31 minutes. The UCAT Decision Making subtest measures your ability to apply logic to reach a conclusion, evaluate arguments and analyse data
This subtest reflect how, as a health professional, you must be able to identify patterns and make hypotheses based on abstract or incomplete information under challenging time constraints.
In these questions, you are given a passage and you must then respond to a series of questions or statements about the passage.
The following problem types are explored in the Decision-Making subtest:
- Logical Puzzles
- Syllogisms
- Interpreting information
- Strongest argument questions
- Venn Diagrams
- Probabilistic Reasoning
In this article, we will be focusing on the following two problem types:
- Venn diagrams
You will be required to interpret a Venn diagram or construct a Venn diagram from the information provided. There may be a lot of quick arithmetic involved as well, and at times using the pen and paper will be a lot quicker than using the on screen calculator. The questions mean you will be:
- Presented with a Venn Diagram, choose the single best conclusion from a variety of statements
- Presented with a passage of information that you can interpret as a Venn Diagram. You will then be asked to choose the one single best solution from a selection of statements.
- You’re given a list of statements where you need to choose a Venn Diagram that best represents information correctly.
Venn Diagram questions are multiple choice questions.
- Strongest argument
These questions ask you to evaluate arguments for and against a particular solution to a problem. They are usually about a public issue or a topical passage.
Make sure that the argument you select addresses the concern in the question – all answers might seem relevant but not all will address the particular argument at hand. Don’t let your personal bias affect your choices – eliminate all the assumptions rather than statement of facts!
Recognising Assumption / Strongest argument questions are multiple choice questions.

Sample problem 1 (Venn diagram):
The diagram below represents the instrument(s) that students from a music school in New York play. It also indicates the duration and frequency of their practice sessions each week. Students must practice at least once a week.
Question
The circle represents students who play the cello.
The rectangle represents students who play the piano.
The triangle represents students who practice for more than 4 hours.
The oval represents students who practice less than 2 days a week.
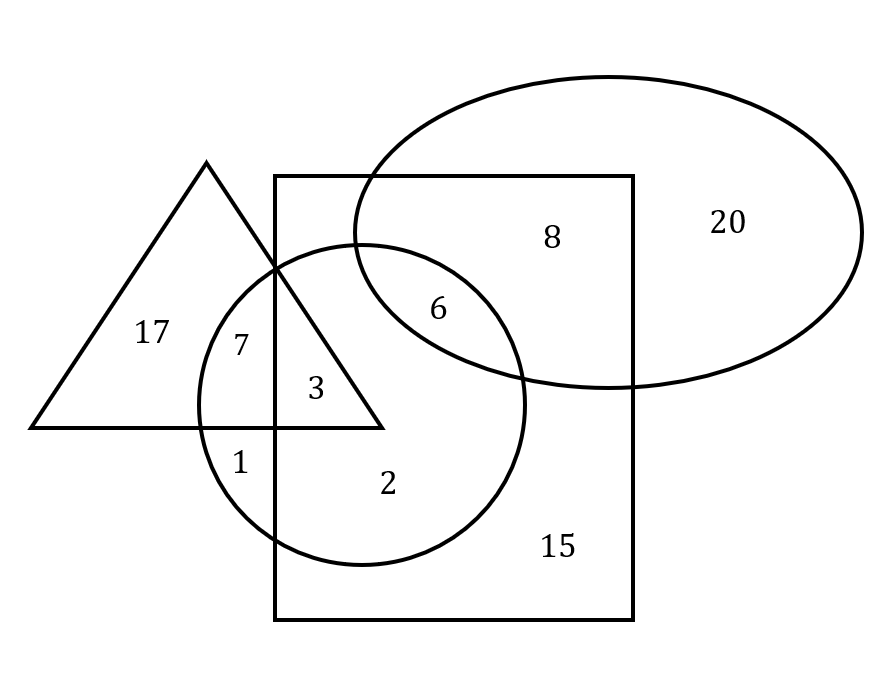
Which of the following statements is true?
- The total number of students who practice for less than 2 days a week for three hours is 6.
- The total number of students who exclusively play the piano is 15.
- The number of students who play both the cello and piano and practice for 5 or more hours is half the number of students who play both the piano and cello for one day a week.
- The number of students who play the cello and practice for six hours, three days a week, is half the number of students who practice for one day a week.
Solution:
- Option (a) is incorrect because all students in the oval practice exactly one day a week, which is a total of 34 students instead of 6.
- Option (b) is incorrect because it is not clear whether the 15 students that play the piano, but not the cello, also do not play any other instruments. This diagram can only verify whether or not students play the piano and/or the cello, but does not tell us anything else.
- Option (c) is correct since the number of students that play both the cello and the piano for more than 4 hours (which is 5 or more hours) is 3, and the number of students that play both instruments and practice only once a week is 6. (It is exactly once a week since it they practice less than two days a week, and all students must practice at least once a week).
- Option (d) is incorrect since there are only three (possible) students who play both instruments and practice for six hours, three days a week, but the number of students that practice exactly once a week is 34 (as mentioned in the explanation for option (a)).
Sample problem 2 (Venn Diagram):
Question
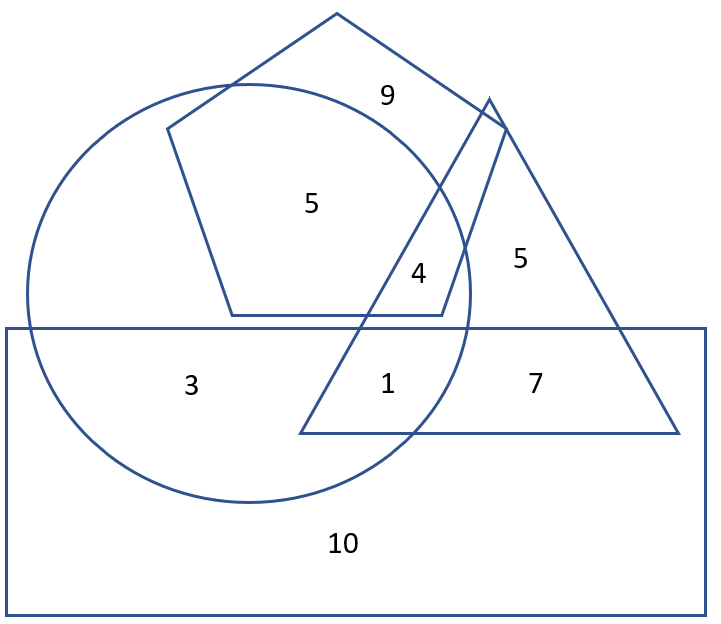
The Venn Diagram above represents different groups of people as follows:
- The circle represents university-educated individuals
- The triangle represents married individuals
- The rectangle represents people who are currently employed
- The pentagon represents those who feel they are stressed.
Which one of these statements is true?
- Four people are stressed about their marriage
- University educated individuals were generally more likely to have a job than non-university educated individuals
- The number of people currently employed and married is greater than the number of stressed employees.
- There are double the number of stressed individuals in marriages than there are married university-educated individuals.
Solution
- Four people are stressed AND are married but not necessarily due to their marriage
- There are 4 people who are university-educated and currently employed, whilst there were 17 employed individuals who were non university-educated.
- This is the correct answer. The number of people currently employed and married (8) is greater than the number of people who feel they are stressed and employed (0).
- There are four stressed individuals in marriages. There are five married university-educated individuals.
Sample problem 3 (Venn Diagram):
A group of children were surveyed on some films. W is the set that liked Shrek. X is the set that liked Toy Story. Y is the set that liked Up.
Some of the older children (Group Z) found they liked both Shrek and Toy Story, as those films were a bit older. Nobody liked all four films.
Question
Which of the following Venn Diagrams best represents the above information?
a.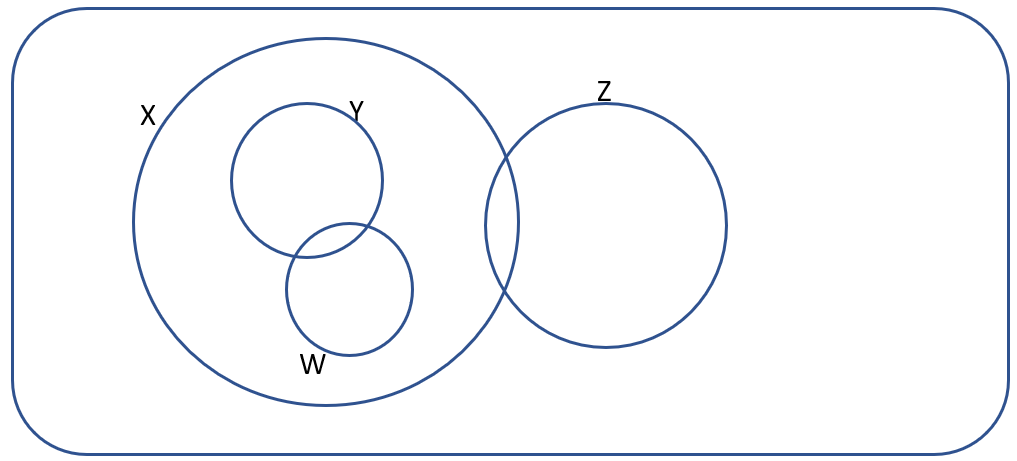
b.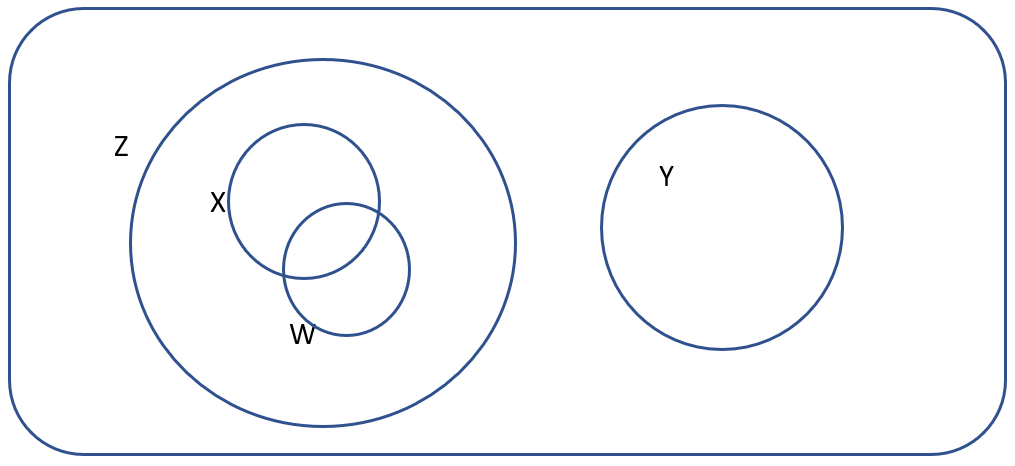
c.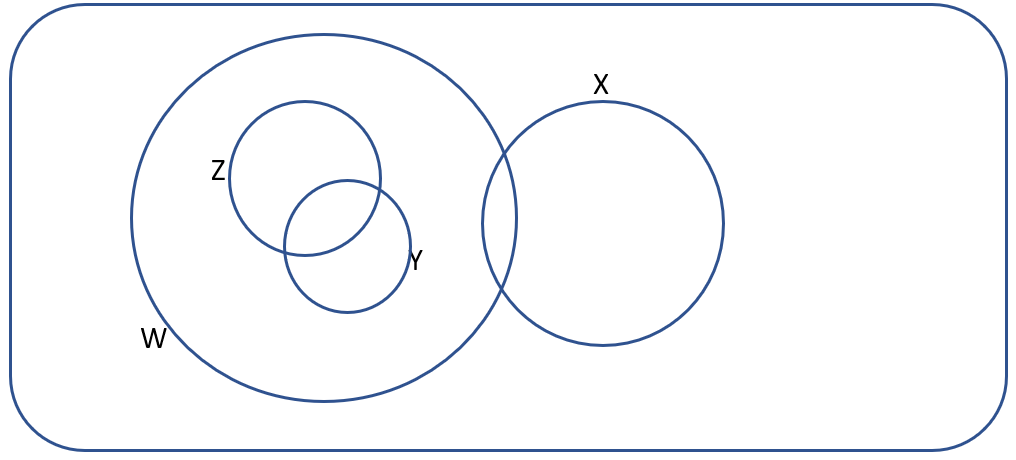
d.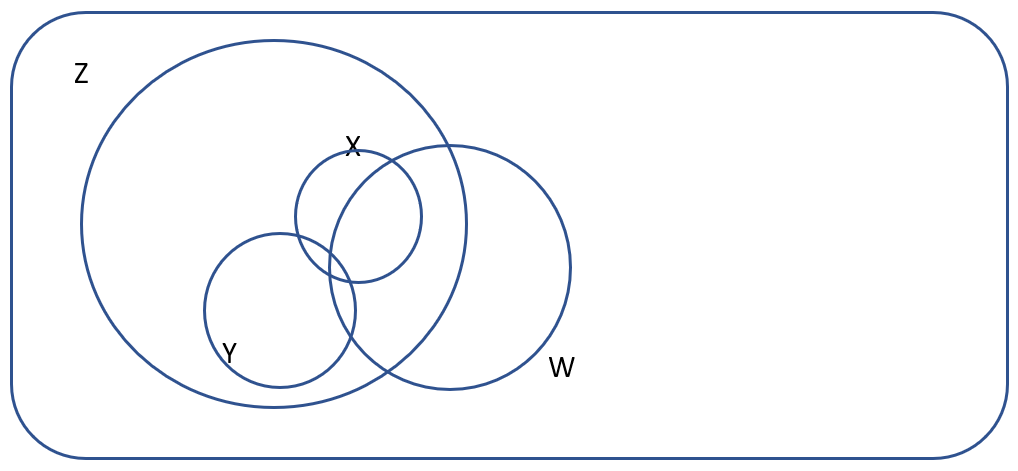
Solution:
- Answer (a) is incorrect. This diagram implies that some older children (group Z) only liked Toy Story (group X) when it’s stated that some older children liked both Shrek (group W) and Toy Story (group X).
- Answer (b) details the information correctly. Whilst it isn’t specified that children who like Up (group Y) don’t like any of the other films, or that children who like Shrek (group W) also happen to like Toy Story (group X), the information it gets correct from what’s provided in the question is that “Some of the older children (Group Z) found they liked both Shrek and Toy Story”.
- Answer (c) is incorrect as the diagram implies that some older children (group Z) who like Up (group Y) and children who like Up also happen to like Shrek (group W). This isn’t stated anywhere in the question.
- Answer (d) is incorrect as it implies that some older children like all the movies stated, which is not provided in the question.

Sample problem 4 (Strongest Argument):
Question
Is it the responsibility of social media influencers to use their influence to encourage viewers to stay home during the COVID-19 lockdown period as announced by the government?
- Yes, because social media influencers should encourage their viewers to abide by the government.
- Yes, because they should be influencing their viewers for the good of society.
- No, because viewers are allowed to do what they want.
- No, because social media influencers are not obligated to advocate government directives.
Solution
- Option (a) is incorrect, since the question is about responsibility, and the option is an opinion about what social media influencers are supposed to do.
- Option (b) is incorrect because this is also an opinion on what social media influencers should be doing, instead of addressed whether they are required to do so.
- Option (c) is incorrect as the question is asking whether it is the responsibility of social media influencers to encourage viewers to stay at home, not whether it is the obligation for viewers to do so.
- Option (d) is correct as it answers the question by addressing that social media influencers are not responsible for the promotion of government directives with an objective reason (because they are not obligated on legal or moral grounds to do so).
Sample problem 5 (Strongest Argument):
Question
Should voting remain compulsory in all local, state and federal elections to ensure that governments are a true representation of the population’s values and ideals?
Select the strongest argument.
- Yes, people should cherish enfranchisement and therefore should exercise their rights as much as possible
- Yes, compulsory voting allows the passage of legislation that reflects the will of the people
- No, Australia is a democracy and people should be allowed to choose if they want to exercise a particular right
- No, governments will never be a true representation of society
Solution
- Option (a) is incorrect. This answer refers to enfranchisement, which was not brought up in the argument.
- Option (b) is the correct answer. It addresses both key issues within the argument presented; compulsory voting and the representation of values and ideas.
- Option (c) is incorrect. This argument does not reflect the crux of the argument presented, as it debates whether the right should be exercised at an individual’s discretion. We need to focus on the effectiveness from exercising enfranchisement.
- Option (d) is incorrect. Whilst this answer addresses the argument presented, it projects a personal view.
Want to practice Decision Making with an online simulator?
UCAT Masterclass uses an accurate simulator with customisable test banks to help you practice the sections your weakest at. Try a free trial now!
