UCAT Advice Quantitative Reasoning
4 Must-Dos to Ace the Quantitative Reasoning Subtest
Do you struggle with quantitative reasoning questions? Does the time pressure cause you anxiety? In this article, we’ll show you 4 must-dos to ace the Quantitative Reasoning subtest.
What is Quantitative Reasoning?
Quantitative Reasoning is one of the UCAT subtests and tests your ability to process numerical problems in a short time.
The questions involve simple numerical operations like addition/subtraction/division/multiplication, and typically cover the following topics:
- Table reading
- Chart / Graph reading
- Percentages
- Averages: means, modes and medians
- Ratios and proportionality
- Rates and Converting rates
- Perimeters, areas and volumes
The Quantitative Reasoning subtest contains 36 questions, which must be completed in 24 minutes, which translates to 30-40 seconds per question. Each question consists of five multiple choice options arranged in increasing order. Occasionally, the fifth option is “Can’t tell,” which allows for the possibility that the question cannot be answered from the information given.
If you’d like a more detailed break down of the Quantitative Reasoning Subtest, you should read our detailed Guide.
The questions are mostly arranged in groups of four, where each group relates to the same information. There are also around four standalone questions.
4 Must-dos to ace the Quantitative Reasoning Subtest
The level of mathematics required for Quantitative reasoning is not difficult (typically corresponding to year 10 or below) – but this not a maths test! The difficulty comes from the time pressure, the amount and complexity of information, and the complexity of the questions.
Keep these tips in mind when preparing for Quantitative Reasoning:
1. Mental mathematics
It’s not enough to be able to answer a question – you must be able to do it in 30-40 seconds per question. It’s important to be efficient and keep track of time to make sure you can get through all the questions. The best way to do this is to be able to instinctively perform quick mental calculations when reading a question.
2. Eyeball answers and eliminate options
Learn to identify the obvious incorrect answers or eliminate the obvious incorrect answers. For example, if values are too big or too small, or if values have increased or decreased relative to something. Picking up on these things will help you to narrow down the answer options or identify the answer altogether.
3. Attention to detail
You must be able to filter out information that is not beneficial to answering the question and identify useful information. Get into the habit of quickly jotting down important information.
Information and questions will usually be presented in a complicated way, so attention to detail is important in correctly interpreting what is presented or asked.
Also, be careful of the UCAT on-screen calculator as it does not follow order of operations like a scientific calculator.
4. Be able to effectively utilize mathematical principles
Make sure you’re up to speed with the topics listed above and can proceed to calculations immediately. If you’re spending time thinking about how to perform a calculation, then you need more practice. The calculations should become second nature to you.
Also be careful of the correct conversion of units as there may be many unit changes taking place within a particular question. Make sure quantities are in the correct units before you finalise your calculations.
Let’s consider how to work through a sample question.
How to use these 4 must-dos to ace the quantitative reasoning subtest
Now you know what you need to do, let’s show you how to do it.
This question is in the more common format of four questions referring to the same information. This particular question present the information using text and a diagram, but remember that text only, charts, and tables are also common.
Mary and Andrew live in Sydney and wish to visit a friend in Melbourne. They decide to drive and visit a couple of sites along the way. At one point in the trip in between Canberra and Mount Kosciuszko, Mary and Andrew take a break. Below is a map of the sites visited on the way to Melbourne:
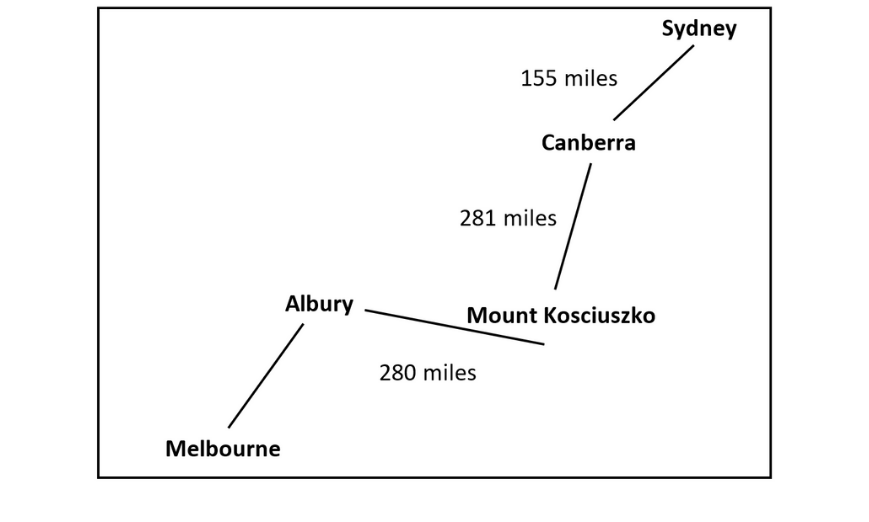
Question 1
If the speed limit between Canberra and Mount Kosciuszko was 110 \text{km/hr} and Mary and Andrew drove at the speed limit, how long did it take them to get from Canberra to Mount Kosciuszko?
(a) 2 hours 55 minutes
(b) 3 hours 33 minutes
(c) 4 hours 5 minutes
(d) 4 hours 9 minutes
(e) Can’t tell
You might be tempted to work it out. First you might convert miles to kilometers:
281 \text{ miles} \times 1.6 = 449.6 \text{km}
Then, using \text{Time}=\frac{\text{Distance}}{\text{Speed}}, you might find the time:
T=\frac{449.6}{110}=4.09 \ \text{hours} = 4 \ \text{hours and } 5 \ \text{minutes}.
However, this is incorrect. Attention to detail is required:
The question stimulus says that they took a break on that leg of the trip, and the length of the break is unspecified.
Therefore the answer is (e) Can’t tell.
The other answer options would correspond to specific mistakes or misunderstandings. For example, if the distance in miles was used instead of the distance in kilometers, or if 4.09 hours was incorrectly interpreted as 4 hours and 9 minutes.
Question 2
How far is Melbourne from Albury if the drive takes 3 hours and 40 minutes at a speed of 90 \text{km/hr}?
(a) 191 miles
(b) 206 miles
(c) 306 miles
(d) 330 miles
(e) 528 miles
This question relies on effectively applying mathematical principles and unit conversions.
The speed is in given in hours, but the time taken is given in hours and minutes. To make things consistent, convert 3 hours and 40 minutes into hours:
40 \ \text{minutes} = \frac{40}{60} of an hour, therefore the total time taken is 3 \frac{2}{3} = 3.667 \ \text{hours}.
Then you can find the distance using D = S \times T
D = 90 \times 3.667 =330 \text{km}All the answer options are in miles, so convert 330 \text{km} into miles:
330 ÷ 1.6 = 206 \text{miles}Therefore, the answer is (b).
The other answer options relate to various numerical errors, such as not converting to miles, or converting to miles incorrectly.
Question 3
Mary and Andrew wonder if they should have also driven from Albury to Shepparton on the way to Melbourne. By what percentage would that increase the length of the trip, not including the last leg to Melbourne, if Shepparton is 174.4 \ km from Albury?
(a) 13.2\%
(b) 15.2\%
(c) 24.4\%
(d) 37.7\%
(e) 56.9\%
Find the length of the original trip, not including the last leg to Melbourne. Use mental arithmetic:
155 + 281 + 280 = 716 \text{miles}.
Convert Albury-to-Shepparton distance to miles:
174.4 ÷ 1.6 = 109 \text{miles}.
The modified trip (excluding Melbourne) would be 716 + 109 = 825 \text{miles} (mental arithmetic).
The percentage increase is:
\frac{825}{716} -1 = 15.2\%Therefore, the answer is (b).
The other answer options correspond to specific mistakes, such as failing to convert the 174.4 km to \text{miles}, or incorrectly calculating the percentage increase.
For this question, you could also consider eyeballing the answer.
The original distance is roughly 700 \text{miles}, and the distance increases by 100. 100 out of 700 is 1 out of 7, which is 14%. This should narrow it down to the first two answers. Considering the increase is 109, which is greater than 100, should lead you to picking the value closest to but larger than 14%, which is the correct answer.
Question 4
Mary decides to play some podcasts in the car between Sydney and Canberra. If the average speed was 95 km/hr, and each podcast was 25 minutes long, how many podcasts did Mary and Andrew complete?
(a) 3
(b) 3.9
(c) 5
(d) 6
(e) 6.3
The distance from Sydney to Canberra is 155 miles which should be converted to 155 \times 1.6 = 248 km.
The time the trip takes is \text{Time}=\frac{\text{Distance}}{\text{Speed}}=\frac{248}{95}=2.61 \text{hours} = 2.61 \times 60 \text{minutes} = 156.63 \text{minutes}.
The number of podcasts they get through is 156.63 ÷ 25 = 6.26.
However, attention to detail is required. The question asks how many they completed, so the answer is (d) 6.
The other answer options again rely on common errors, such as incorrect unit conversions, or not considering how many podcasts were actually completed.

