UCAT Advice Quantitative Reasoning
How to Ace UCAT Perimeter and Area or Chart and Graph Questions | Quantitative Reasoning Subtest
Do you get stressed out trying to solve perimeter and area questions for the quantitative reasoning subtest? Do you run out of time or get confused with chart and graph questions? Don’t worry, in this article, we going to show you how to ace these types of Quantitative Reasoning subtest questions.
What common issues do UCAT students share in the Quantitative Reasoning subtest?
Students that sit the Quantitative subtest typically tend to struggle with the following:
- Time constraints. Students are unable to use the calculator at the UCAT examination centers effectively to maximize efficiency.
- Attention to detail. Students struggle with identifying key pieces of information and glazing over the irrelevant details to maximize efficiency.
Students may confuse formulas/steps when trying to solve the questions quickly. Training speed and accuracy together is only possible with practice under timed conditions!
Overall, the biggest struggle for students who sit this subtest is time management. Learning strategies and techniques which minimize time wastage and maximize efficiency will assist you in acing the exam!
So how do I fix this?
One strategy to improve your time management is to systematically break down complex questions into basic steps. This makes your thinking clearer and workflow faster. By going through some difficult sample questions, this article will demonstrate by example exactly how you can do this yourself with fully worked solutions.
Want to see where you’re at with the UCAT?
What problem types will I have in the QR subtest?
The following problem types are explored in the Quantitative subtest:
- Table reading
- Chart / Graph reading
- Percentages
- Averages: means, modes and medians
- Ratios and proportionality
- Rates and Converting rates
- Perimeters, areas and volumes
In this article, we’ll be digging into:
Perimeters, areas and volumes
The diagram (not to scale) below outlines the floor plan for a collection of new apartments:
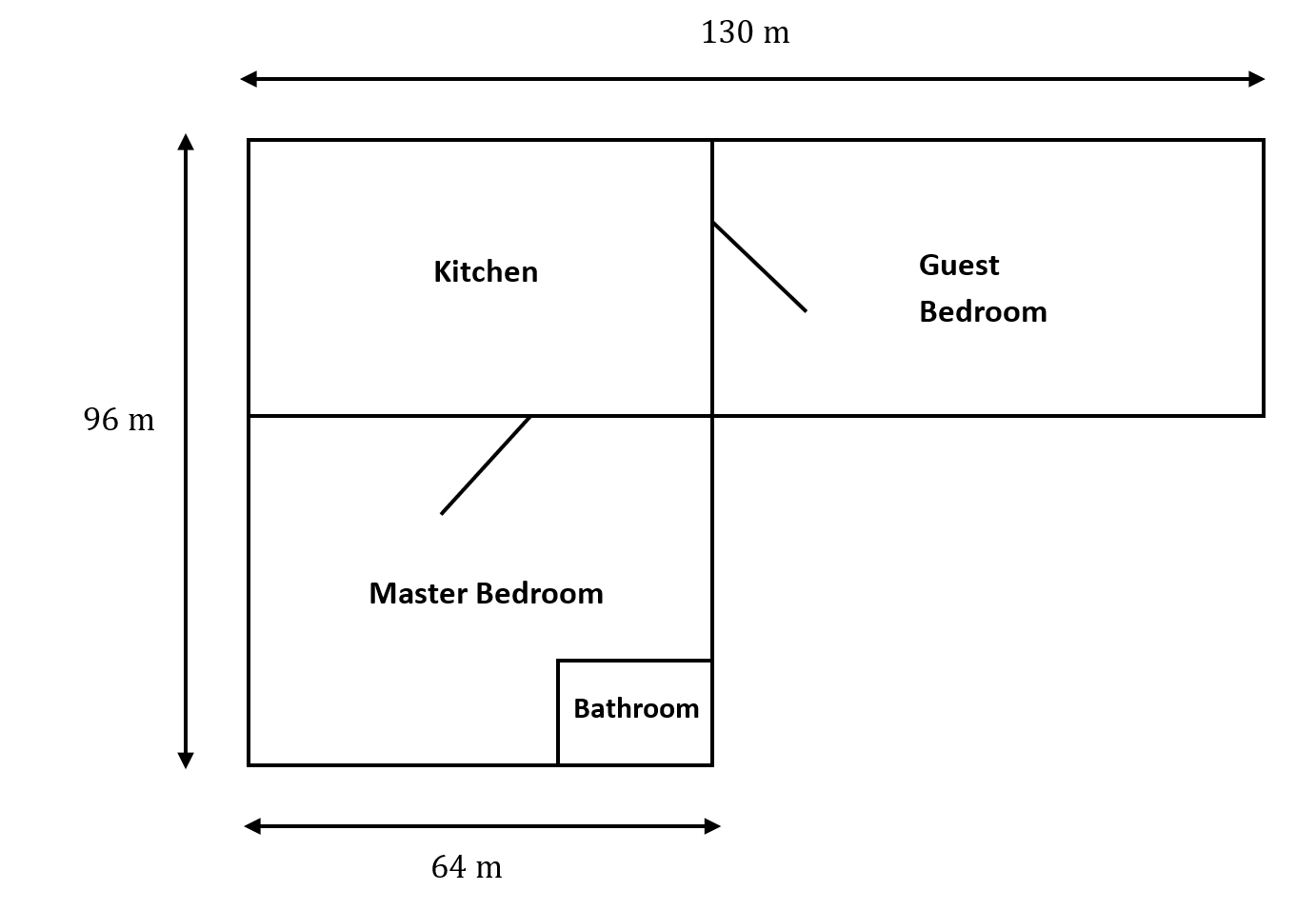
- The bathroom makes up 25\% of the combined area of both the kitchen and the guest bedroom.
- The cost of covering the floors with carpeting is priced at \$6 per square metre, or \$9.50 per square metre for tiling.
Question 1:
If the area of the kitchen is 390 \text{ m}^2 smaller than the area of the master bedroom, what is the area of the kitchen, in square metres?
- 2877 \text{ m}^2
- 3267 \text{ m}^2
- 5754 \text{ m}^2
- 6144 \text{ m}^2
Solution: A
Step 1:
The tricky part of this question is that finding the width of the kitchen and master bedroom is not given so it’s important to find the total area of both the kitchen and master bedroom first:
96×64=6144 \text{ m}^2
∴K+M=6144
Step 2:
The next part of this question is using the information provided in the question, which is that the kitchen is 390 \text{ m}^2 smaller than the master bedroom.
∴M=K+390Step 3:
The last part is to solve the two equations generated from the question simultaneously:
K+M=6144
M=K+390
∴K+K+390=6144
2K=5754
K=2877 \text{ m}^2
Question 2:
If the perimeter of the master bedroom (including the bathroom) is 390\text{ m}, what is the total area of the bathroom and guest bedroom?
- 845 \text{ m}^2
- 963 \text{ m}^2
- 1274 \text{ m}^2
- 2561 \text{ m}^2
- 6895 \text{ m}^2
Solution: D
Step 1:
Use the information about the perimeter to determine the dimensions of the master bedroom. Let x be the length of the left side of the master bedroom.
Then, we have
2x+2(64)=268
2x=140
x=70
Step 2:
Find the area of the bathroom first, which would require the combined area of the kitchen and the guest bedroom.
Since the left side length of the master bedroom and the left side length of the kitchen sum to 96 \text{ m} , we know the left side length of the kitchen is 96-70=26 \text{ m} .
Hence, the combined area of the kitchen and the guest bedroom is 26×130=3380 \text{ m}^2 .
The area of the bathroom is thus 25\%×3380=845\text{ m}^2.
Step 3:
Find the area of the guest bedroom. From Step 2 the left side length of the guest bedroom is the same as the left side length of the kitchen, which is 26.
The top side of the guest bedroom has length 130-64=66 \text{ m} and so the area of the guest bedroom is 66×26=1716 \text{ m}^2.
Step 4:
Find the total area.
The combined area of the bathroom and the guest bedroom is 845+1716=2561 \text{ m}^2.
Question 3:
If the length of the left side of the kitchen is 50\text{ m}, what is the length of the left side of the bathroom?
- 5 \text{ m}
- 5 \text{ m}
- 6 \text{ m}
- 0 \text{ m}
- Can’t Tell
Solution:
There is actually not enough information to determine the answer to this. It’s not stated that all the rectangles are in perfect similarity with each other nor are any one of the dimensions of the bathroom provided. Hence, the solution is Can’t tell.
A common mistake would be to do 50×25\%, but this is not necessarily true. Just because the area of the kitchen is 25\% of the combined area of the kitchen and guest bedroom, does not mean the side length of the bathroom is 25\% of the side length of the kitchen/guest bedroom.
Question 4:
The owners of the apartment decide to place carpeting across the entire apartment except for the bathroom and decide to place tiling across the bathroom. What is the total cost to do this if the area of the kitchen was 3264 \text{ m}^2?
- \$7335.00
- \$54195.5
- \$62861.25
- \$72806.25
- Can’t Tell
Solution: C
Step 1:
Use the area of the kitchen to find the length of the left side of the kitchen.
Since left side length ×64=3264 \text{ m}^2, the left side length must be 51\text{ m}.
Step 2:
Find the area of the kitchen and the guest bedroom. Since the side length is 51, the area must be 51×130=6630 \text{ m}^2.
Step 3:
Use the combined area of the kitchen and the guest bedroom to find the area of the bathroom.
The area of the bathroom is 25 \%×6630=1657.5.
Step 4:
Using the side length of the kitchen, find the side length of the master bedroom and find its area (less the area of the bathroom).
The side length of the master bedroom is 96-51=45 \text{ m} .
The combined area of the master bedroom and the bathroom is 45×64=2880 \text{ m}^2
Hence the area of the master bedroom alone is 2880-1657.5=1222.5 \text{ m}^2.
Step 5:
Use the areas found in Step 1 to 4 to find the total cost.
The carpeting for the kitchen and the guest bedroom will cost 6630 \text{ m}^2×\$6 / \text{ m}^2=\$39780
The carpeting for the master bedroom will cost 1222.5 \text{ m}^2 ×\$6/ \text{ m}^2=\$7335
The tiling for the bathroom will cost 1657.5 \text{ m}^2×\$9.50/ \text{ m}^2 =\$15746.25
Hence, the total cost is 39780+7335+15746.25=\$62861.25
Chart / Graph reading
The chart below provides information on a large gym organization and the profits it made from different cities in Australia.
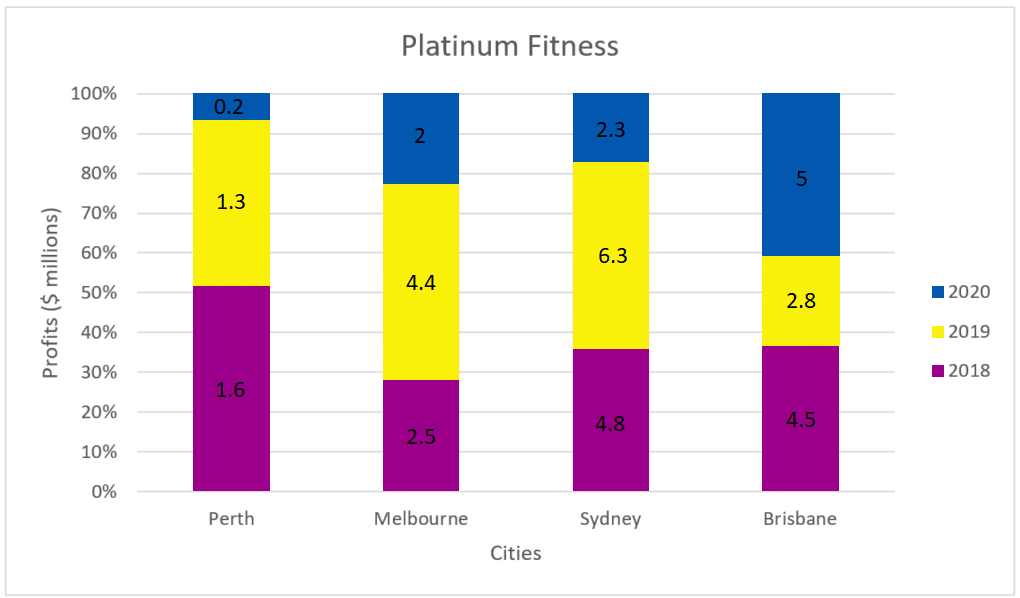
Profit figures are in millions of dollars. For example, 2.3 would be referring to 2.3 million dollars.
Question 1:
Which city made the highest total profit for all three years?
- Perth
- Melbourne
- Sydney
- Brisbane
- Can’t Tell
Solution: C
To save time for this question, use the eyeball method or quick basic arithmetic to determine that Sydney is the city which made the most profit.
Question 2:
How much profit did Platinum Fitness make in Australia in 2020?
- 9.5 million
- 12.6 million
- 14.88 million
- 13.4 million
- 37.7 million
Solution: A
This would be the sum of the figures in grey (which represent the profit made in 2020 in each city): 0.2+2+2.3+5=9.5 million.
Question 3:
What is the percentage change in profit from 2018 to 2019 in Sydney?
- -63.49%
- -31.25%
- 31\%
- 25\%
- 49\%
Solution: D
\text{Percentage Change}=\frac{\text{New profit}-\text{Old Profit}} {\text{Old profit}} ×100
=(6.3-4.8)/4.8×100
=31.25\%
Question 4:
Express the profit made by Melbourne in 2018 as a percentage compared to the total profit made by all cities in 2018.
- 63\%
- 66\%
- 05\%
- 73\%
- 09\%
Solution: B
Step 1:
Find the total profit.
The profit made by Melbourne in 2018 is: 2.5 million .
The total profit made by all cities in 2018 is: 1.6+2.5+4.8+4.5=13.4 million.
Step 2:
Calculate Melbourne’s profit as a percentage of the total.
The percentage is \frac{2.5}{13.4}×100=18.66\%
